अध्याय छः

काम, ऊर्जा

और शक्ति

एमसीक्यू I

6.1 एक इलेक्ट्रॉन और एक प्रोटॉन एक-दूसरे पर संयुक्त बलों के प्रभाव में चल रहे हैं। गति के दौरान प्रणाली की किनेटिक ऊर्जा में परिवर्तन की गणना करते समय, व्यक्त गणना एक दूसरे पर चुंबकीय बल को नजरअंदाज करता है। यह इसलिए है क्योंकि,

(a) दो चुंबकीय बल बराबर और विपरीत हैं, इसलिए वे कोई परिणाम नहीं प्रदर्शित करते हैं।

(b) चुंबकीय बलों का किसी भी कार्य को समझाना अच्छा नहीं होता है।

(c) चुंबकीय बलों ने प्रत्येक खण्ड पर बराबर और विपरीत (लेकिन गैर-शून्य) कार्य किया है।

(d) चुंबकीय बल अनिवार्य रूप से अनुपेक्षित होते हैं।

6.2 एक प्रोटॉन आराम से रखा जाता है। एक सकारात्मक आधारित तत्व इसके क्षेत्र में से आराम से मुक्त होते समय एक दूसरे में संतुलित और एक पोजाइट्रॉन के मामले में अनुभव किए जाते हैं। समय $t$ में, दो चलते हुए आराम से निर्धारित तत्वों पर कार्य किया जाता है

(a) दोनों परीक्षाओं में लागू किसी भी बल कानून के अनुसार है।

(b) एक पॉजिट्रॉन के मामले में कम होता है, क्योंकि पॉजिट्रॉन अधिक तेजी से दूर जाता है और उस पर बल कमजोर होता है।

(c) दूसरे मामले में पॉजिट्रॉन के मामले में अधिक होता है, क्योंकि पॉजिट्रॉन एक बड़े दूरी तक चलता है।

(d) स्थिर प्रोटॉन पर चार्जयुक्त तत्व द्वारा किया गया काम जैसा ही।

6.3 एक आदमी जमीन पर मूड़ रहा है और उठकर खड़ा हो जाता है। प्रक्रिया के दौरान आदमी पर जमीन का प्रतिक्रिया बल है

(a) मात्रा में $\mathrm{mg}$ के बराबर और स्थिर।

(b) मात्रा में $\mathrm{mg}$ से अधिक और स्थिर।

(c) बदलता है लेकिन हमेशा $\mathrm{mg}$ से अधिक।

(d) पहले $\mathrm{mg}$ से अधिक होता है, और बाद में $\mathrm{mg}$ के बराबर हो जाता है।

6.4 एक साइकिलिस्ट $10 \mathrm{~m}$ में एक छलावा रोककर खड़ा होता है। इस प्रक्रिया के दौरान, सड़क के कारण साइकिल पर बल $200 \mathrm{~N}$ होता है और यह गति के विरुद्ध होता है। साइकिल द्वारा सड़क पर किया गया काम है

(a) $+2000 J$

(b) $-200 \mathrm{~J}$

(c) शून्य

(d) $-20,000 J$

6.5 एक शरीर गुरुत्वाकर्षण के कारण मुक्त रूप से गिर रहा है। निम्न में से कौन सी राशियाँ गिरावट के दौरान स्थिर रहती हैं?

(a) किनेटिक ऊर्जा।

(b) संभावित ऊर्जा।

(c) कुल यांत्रिक ऊर्जा।

(d) कुल रैखिक प्रसारणशक्ति।

6.6 दो शरीरों के बीच असंरेक्षणीय संघर्ष के दौरान निम्नलिखित में से कौन सी राशियाँ हमेशा संरक्षित रहती हैं?

(a) कुल गतिक ऊर्जा।

(b) कुल यांत्रिक ऊर्जा।

(c) कुल रैखिक प्रसारणशक्ति।

(d) प्रत्येक शरीर की गति।

6.7 दो ढीले संरेखित निरतिचल ट्रैक, एक सतत और दूसरा नीचे से आयोजित होते हैं, जो चित्र 6.1 में दिखाए गए हैं।

चित्र 6.1

निम्नलिखित में से कौन सा कथन सही है?

(a) दोनों पत्थर समय पर नीचे पहुंचते हैं, लेकिन उनकी गति समान नहीं होती है।

(b) दोनों पत्थर एक ही गति से नीचे पहुंचते हैं और पत्थर I पत्थर II से पहले नीचे पहुंचता है।

what is the hi version of content: (c) Both the stones reach the bottom with the same speed and stone II reaches the bottom earlier than stone I.

(d) Both the stones reach the bottom at different times and with different speeds.

6.8 The potential energy function for a particle executing linear SHM is given by $V(x)=\frac{1}{2} k x^{2}$ where $k$ is the force constant of the oscillator (Fig. 6.2). For $k=0.5 \mathrm{~N} / \mathrm{m}$, the graph of $V(x)$ versus $x$ is shown in the figure. A particle of total energy $E$ turns back when it reaches $x= \pm x_{m}$. If $V$ and $K$ indicate the P.E. and K.E., respectively of the particle at $x=+x_{m}$, then which of the following is correct?

Fig. 6.2

(a) $\quad V=\mathrm{O}, \quad K=E$

(b) $\quad V=E, \quad K=O$

(c) $V<E, \quad K=\mathrm{O}$

(d) $\quad V=\mathrm{O}, \quad \mathrm{K}<\mathrm{E}$.

6.9 Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed $V$ as shown in Fig. 6.3.

$V$ Fig. 6.3

If the collision is elastic, which of the following (Fig. 6.4) is a possible result after collision?

$V=0$

$V / 2$

(a)

(b) (c)

(d)

Fig. 6.4

6.10 A body of mass $0.5 \mathrm{~kg}$ travels in a straight line with velocity $v=a$ $x^{3 / 2}$ where $a=5 \mathrm{~m}^{-1 / 2} \mathrm{~s}^{-1}$. The work done by the net force during its displacement from $x=0$ to $x=2 \mathrm{~m}$ is

(a) $1.5 \mathrm{~J}$

(b) $50 \mathrm{~J}$

(c) $10 \mathrm{~J}$

(d) $100 \mathrm{~J}$

6.11 A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in Fig. 6.5 correctly shows the displacement-time curve for its motion?

(a)

(b)

हिसाब साझाकरण!

(c)

(d)

चित्रा 6.5

6.12 चित्रा 6.6 में दिखाए गए आरामदायक पथ में सूर्य के चारों ओर धरातल की काइनेटिक ऊर्जा के प्रतिच्छाय को सबसे करीब दिखाने वाली डायग्राम

(ए)

(ब)

(सी)

(डी)

चित्रा 6.6

6.13 चित्रा 6.7 में दिखाए गए डायग्राम में वायु में तीरमद द्वारा यातायात करने वाले एक पेंडुलम की कुल यांत्रिकी ऊर्जा के प्रतिच्छाय को संकेत करता है

(ए)

(सी)

(डी)

चित्रा 6.7

6.14 यदि एक द्रव्यमान $5 \mathrm{~kg}$ वाली एक परिधि $1 \mathrm{~m}$ रेडियस की व्यासमान परिक्रमा करता है, तो अगर द्रव्यमान 300 परिक्रमण प्रति मिनट के साथ चलता है, तो उसकी काइनेटिक ऊर्जा होगी

(ए) $250 \pi^{2}$

(ब) $100 \pi^{2}$

(सी) $5 \pi^{2}$

(ड) 0

6.15 जब आकाश से $h$ की ऊंचाई से गिरता हुआ बूंद आंतरिकीय वेग कहलाने वाली वेगवर्धकता तक इधर उतरता है तब उसकी पोटेंशियल और काइनेटिक ऊर्जा में परिवर्तन सिद्ध करने वाला दिखाई गया दियानिक ग्राफ कौन सा सही तरीके से दिखाता है?

(ए)

(ब)

(सी)

(ड)

चित्रा 6.8

६.१६ एक शॉटपुट क्रियाकलाप में एक खिलाड़ी एक शॉटपुट को $10 \mathrm{~kg}$ के मास में $1 \mathrm{~m} \mathrm{~s}^{-1}$ की प्रारंभिक गति के साथ, भूमि से $1.5 \mathrm{~m}$ ऊपर से $45^\circ$ के आंतरिक वेग से फेंकता है। यदि थोहरा हवा प्रतिरोध को नजरअंदाज करते हुए और गुरुत्वाकर्षण के कारण ऊबरन $10 \mathrm{~m} \mathrm{~s}^{-2}$ हो, तो शॉटपुट धरती को पहुंचते ही किनेटिक ऊर्जा होगी

(ए) $2.5 \mathrm{~जूल}$

(ब) $5.0 \mathrm{~जूल}$

(क) $52.5 \mathrm{~जूल}$

(ड) $155.0 \mathrm{~जूल}$

६.१७ चित्र ६.९ में से किस चित्र में एक आयरन गोला एक झील में स्वतंत्र रूप से गिरते समय किनेटिक ऊर्जा के परिवर्तन को सही रूप से दिखाता है?

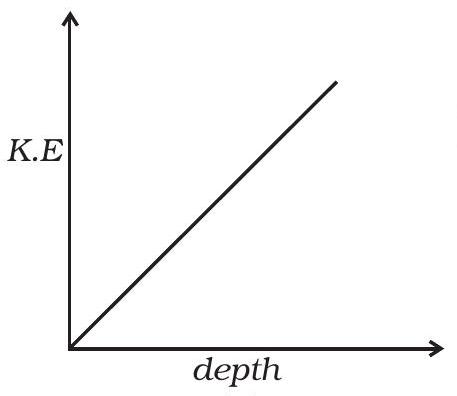
(क)

(ख)

(ग)

(घ)

चित्र ६.९

६.१८ एक क्रिकेट गेंद $150 \mathrm{~ग्राम}$ के मास के साथ $126 \mathrm{~कि.मी.} / \mathrm{घ}$ की गति के साथ बैट के मध्यमें लगातार एक बार स्पर्श किया जाता है, जो खिलाड़ी द्वारा सटीक परिस्थिति में निर्धारित होता है। गेंद गेंद स्पर्श करने के बाद उम्र के साथ टिपटियां बाहर निकलती है। मानते हुए कि गेंद और बैट के बीच संपूर्ण वेगशील एवं इतर टाउचलेस टक्कर है और यह दोनों $0.001 \mathrm{~सेकंड}$ के लिए संपर्क में बने रहते हैं, बैटामार को मजबूती से पकड़ने के लिए खिलाड़ी को लगानी वाली बल कितनी होगी?

(ए) $10.5 \mathrm{~N}$

(ब) $21 \mathrm{~N}$

(क) $1.05 \times 10^{4} \mathrm{~N}$

(ड) $2.1 \times 10^{4} \mathrm{~N}$

एमसीक्यू II

६.१९ एक पुरुष, जिसका भार $m$ है, सीढ़ी के नीचे खड़ा है, जिसकी ऊचाई $L$ है, इसे चढ़ता है और उसके ऊपर खड़ा हो जाता है।

(ए) उस पुरुष पर सभी बलों द्वारा किया गया कार्य उच्चीता में हुए वृद्धि $\mathrm{mgL}$ के बराबर होता है।

(ब) पुरुष पर सभी बलों द्वारा किया गया कार्य शून्य होता है।

(क) पुरुष पर गुरुत्वाकर्षण बल द्वारा किया गया कार्य $m g L$ होता है।

(ड) एक पदब मारने का प्रतिक्रियाशील बल कार्य नहीं करता क्योंकि बल का प्रभास्थान शुन्य होता है जब तक बल मौजूद रहता है।

६.२० एक गोली $म$ भार की, $30^{\circ}$ के साथ आयताकारी गति के साथ आग में से निकलेगी और संपर्क करते हुए एक सॉफ्ट लक्ष्य को, जीमि ऊचाई $h$ के ऊपर होते हुए नीचे आयताकारी रास्ते से निकलती है, इससे पहले की उसकी किंटीक ऊर्जा का आधा हो जाता है।

निम्नलिखित कथनों में से जो सही हैं उनके बारे में कौन सा कथन सही है?

(ए) गोली की वेगवतता अपने प्रारंभिक मान की आधार में आधी कर दी जाएगी।

(ब) गोली की वेगवतता पहले से अधिक होगी।

(क) गोली पहले से ही एक ही पराबोलिक पथ पर चलेगी।

(ड) गोली एक अलग पराबोलिक पथ में चलेगी।

(इ) भारीग्रस्ति को लक्ष्य को मारने के बाद गोलाकार ढंग से नीचे लगेगी।

(फ) लक्ष्य के अणुओं की आंतरिक ऊर्जा बढ़ जाएगी।

6.21 दो ब्लॉक $M_{1}$ और $M_{2}$ जो बराबर भार है, एक आधारशीलता वाली फ्रिक्शनरहित सतह पर गतिशील होने के लिए स्वतंत्र होते हैं। $M_{2}$ को एक निरभार धारी के संपर्क में जोड़ा जाता है जैसा कि चित्र 6.10 में दिखाया गया है। प्रारंभ में $M_{2}$ शांत होता है और $M_{1}$ $v$ की गति के साथ $M_{2}$ के साथ सिरमोचन से टकराता है।

(अ) जबकि धारी पूरी तरह से संपीड़ित होने के दौरान, $M_{1}$ की सभी KE धारी की PE के रूप में संग्रहित होती है।

(ब) जबकि धारी पूरी तरह से संपीड़ित होने के दौरान प्रणाली प्रेरण बरकरार नहीं रहती है, हालांकि अंतिम प्रक्षेपण समयांतरमें मूल प्रमाण बरकरार रहता है।

(क) यदि धारी निर्भार है, तो $M_{1}$ की अंतिम अवस्था शांति की अवस्था होती है।

(ख) यदि खिचड़ीनुमा परिख चल रही है, तो संक्षेप में संघर्ष समस्याग्रस्त नहीं हो सकता है।

चित्र 6.10

VSA

6.22 एक कठोर ढालनी एक स्थिर वेग $u$ वाले एक सारणी पर रखी जाती है जो कि समतल भूमि पर होती है। ढालनी पर मास $M$ का एक ब्लॉक आराम से टिका होता है। ढालनी और ढाली के बीच घर्षण की ताकत के द्वारा कोई कार्य किया जाता है क्या? क्या इसमें ऊर्जा का रिसाव होता है?

6.23 एलिवेटर नीचे आ रहा होने पर क्यों कोई विद्युत शक्ति की आवश्यकता होती है? इस मामले में यात्रियों की संख्या पर कोई सीमा होनी चाहिए?

6.24 एक शरीर को भूमि के सतह से ऊँचाई $h$ तक उठाया जा रहा होता है।

(अ) लागू बल द्वारा किया गया कार्य का चिह्न क्या होगा?

(ब) गुरुत्वाकर्षण बल द्वारा किया गया कार्य का चिह्न क्या होगा?

6.25 एक कार द्वारा भूमि के विरुद्ध गुरुत्वाकर्षण में किया गया कार्य की गणना करें। कार का भर मास $400 \mathrm{~kg}$ है और चले गए दूरी $2 \mathrm{~m}$ है।

6.26 एक शरीर हवा में मानवीय ऊर्जा के साथ पृथ्वी की ओर गिरता है। क्या इसकी कुल यांत्रिक ऊर्जा गिरते हुए बरकरार रहेगी? कारण बताएँ।

6.27 एक शरीर को एक बंद गोल का मार्ग परिभ्रमित किया जाता है। क्या शरीर को ले जाने में कार्य सदैव शून्य होगा? यदि नहीं, तो ऐसी परिस्थिति का उल्लेख करें जिसमें बंद पथ पर यात्रा किया गया कार्य हमेशा शून्य होता है।

6.28 दो बिलियर्ड गेंदों के संपर्क में होने वाले एक कठोर संघर्ष में, निम्न में से कौन सी मात्राएं संघर्ष के छोटे समय के दौरान (अर्थात जब वे संपर्क में हों) संरक्षित रहती हैं।

(अ) ऊर्जा कीनेटिक।

(ब) कुल रैखिक-गति?

प्रत्येक मामले में अपने उत्तर के लिए कारण दें।

6.29 वाट में एक वृक्षारोहण के बल की गणना करें, जो $20 \mathrm{~s}$ में एक $100 \mathrm{~kg}$ के भार को $10 \mathrm{~m}$ ऊँचाई तक उठाता है।

6.30 मानवीय ह्रदय एक बार धड़कने पर औसत कार्य $0.5 \mathrm{~J}$ है। यदि यह मिनट में 72 बार धड़कता है तो उपयोगी कारण गणित करें।

6.31 ऐसी स्थिति का उदाहरण दें जिसमें एक लागू बल न किनेटिक ऊर्जा में कोई परिवर्तन लाता है।

6.32 प्राय: एक समान ऊर्जा वाले दो शरीर समान दिशा में चल रहे होते हैं। उन्हें एक ही मात्रा के पुनरावृत्ति बल को लागू करके बंद किया जाता है। ऐसे में उन दोनों द्वारा संत बनाने से पहले चलाए गए दूरी का कैसा सम्बंध होगा?

बाईं तरफ काट D-ब: (6.33) वेगाली रेखांच्या जवळील पॉईंटिला असेलेले पायपाट

(ब) सीमित क्षेत्र D मध्ये: (6.34)

(ख) हेड-ऑन संघर्षासाठी, दोन सानों गोलाने अग्रेसरा लक्षात जाऊ शकतात. (।) एक खास संघर्षसाठी, दोन गोलाने विस्थापित वेगांच्या दोन दोन्हिके दिशा $90^{\circ}$ पेक्षा कमी आहे. (6.35)

A- क्षेत्री (6) चि.) चित्र दिली आहे. अनुरुप एथॅनॉलच्या संचालनानुसार विभाजन क्षेत्री कोणत्याही एका तत्वाला शोधू शकता की नाही. (6.36)

पंदुल्याच्या वजाबद्दलच्या तथांची ज्ञाने: (D व तक्रार L) (6.37)

(ए ) हंगामीच्या उंचावर बाब A हा मोजण्याच्या उंचावर वाढतो.

(ब) ब बोबला सुरु कीव मारणारा वेग. विस्तारलेल्या ठेवता बोबांचा आकारावरती उपेक्षा करा आणि टक्रार आंकणारा आहे. (6.37)

(ऐ) 1.00जी प्रमाणाच्‍या पाऊसाच्या मागची उंचीकडून वळणारा द्रोप 50प्रमाणांकीत मीटरप्रति सेकंदांच्या वेगांनी जमिनीवर प्रमाणांकीत्या दिला जातो.

(ब) ड्रॉपच्या पसरणाचा क्षेत्र प्रमाणांकीते स्वागत प्रमाणांकीतत्वासाठी नुकतेच प्राप्त करा.

(क) ड्रॉपचा पसरणाचा क्षेत्र प्रमाणांकीते हार प्र.उ.साठी मिळवा. जशी वाट सुरू. (10 प्रतिसेकंद प्रमाणांकचा जी, दुसऱ्यांवरून दिलेलेच खहरा आहे त्यावर प्रस्तावित केलाले आहे.) (6.38)

(ख) आपोआपी बोबसोबतची दोन प्रमाणी मुक्तायत्त केलेलेच मूवमेंट समझण्यासाठी वर्षातील एक अखेर वेळाची वाढ दिली आहे. त्यात, प्रतिप्रमाणी मोमबत्या आणि नियमित चित्वारयात्रेच्या त्यागात घडता आहे. (ब) प्रत्येका पंदुल्याच्या उर्जेच्या प्रमाणांकीत नोंदवायला वेळेची आहे, जी, तब्यत्र आढळत नाही. कुठेही T २ मध्ये 0 क्षेत्रित करा. (सर्व प्रमाणांकीतच्या उंचपणासाठी मदतची आवश्यकता आहे.) (6.39)

अनुवाद:

Fig. 6.14

6.40 मान लीजिए कि वर्ष में $100 \mathrm{~cm}$ वाले स्थान पर पानी गिरता है। छत के प्रति मीटर सतह पर रान के द्वारा स्थानांतरित ऊर्जा की गणना करें, जब रान के औसत मास $3.0 \times 10^{-5} \mathrm{~kg}$ होता है और उनकी औसत अंतिम वेग $9 \mathrm{~m} \mathrm{~s}^{-1}$ होता है।

6.41 एक इंजन को एक बहुत लंबी धमकी लगाई गई है जो $1.5 \mathrm{~m}$ की लंबाई की होती है। प्रणाली का कुल मास $50,000 \mathrm{~kg}$ के साथ $36 \mathrm{~km} \mathrm{~h}^{-1}$ की गति से चल रहा है जब इसे विराम के लिए लगभग स्थिर किया जाता है। प्रणाली को विराम कराने की प्रक्रिया में, धमकी वाले तार का संकोच $1.0 \mathrm{~m}$ हो जाता है। अगर धमकी की $90 %$ ऊर्जा घर्षण के कारण खो जाती है, तो स्प्रिंग संख्यात्मक के मान की गणना करें।

6.42 एक वयस्क $600 \mathrm{~N}$ का वजन होता है और प्रत्येक कदम $1 \mathrm{~m}$ लम्बा होता है। जॉगिंग में उसके द्वारा उपयोग की गई ऊर्जा की गणना करें, अगर वह $6 \mathrm{~km}$ जॉग करता है, मानते हुए कि ज़मीन और हवा के घर्षण के कारण कोई ऊर्जा हानि नहीं होती है। वयस्क की शरीर को 10% भोजन के रूप में उपयोग करने की क्षमता होती है, तो जॉगिंग के लिए उपयोग की गई ऊर्जा के हितों की गणना करें।

6.43 पेट्रोल की पूरी जलन पर $3 \times 10^{7} \mathrm{~J}$ के बराबर ऊर्जा मुक्त होती है। एक परीक्षण चालान में एक गाड़ी जिसका वजन $1200 \mathrm{~kg}$ है, ड्राइवर के मास सहित, एक सीधे ट्रैक पर स्थायी गति के साथ $15 \mathrm{~km}$ चलती है। यदि गाड़ी की इंजन की क्षमता 0.5 होती है, तो परीक्षण चालान के दौरान गाड़ी पर जनित फ्रिक्शन की बालप्रभुता की गणना करें।

ला

6.44 सतह के एक चोटर आंगल जिसमें रुखे पर $30^{\circ}$ होता है पर एक कठोर कर रस्सी से एक $1 \mathrm{~kg}$ भार का ब्लॉक धकेला जाता है (चित्र 6.15)। ब्लॉक को रुखे से $10 \mathrm{~m}$ ऊपर धकेला जाता है, जबकि अम्लीयन तत्संबंधी गुलामी के बीच संपर्क $\mathrm{BCD}$ खंड होता है। यदि गिड़ने के बिना बॉल 1 के पास बहुत बहुत फ्रिक्शन होता है, तो बॉल 2 के पास कम फ्रिक्शन होता है और बॉल 3 के पास उच्चतम फ्रिक्शन होता है।

Fig. 6.16

(a) किन गेंदों के लिए कुल मैकेनिकी ऊर्जा संरक्षित होती है?

(b) डी तक पहुंच सकती है कौन सी गेंद (गेंदें) हैं?

(c) जो गेंदें डी तक पहुंच नहीं पाती हैं, उनमें से कौन सी गेंदें वापस A तक पहुंच सकती हैं?

6.46 एक विमान गैस को नीचे की ओर निकालकर सीधे ऊपर निकलता है। एक छोटे समय अंतराल $\Delta t$ में, यह एक गैस की द्रव्यमान $\Delta m$ को एक अभिक्रिया गति $u$ की रेलेटिव गति पर छोड़ता है। $t+\Delta t$ और $t$ पर पूरे प्रणाली की $\mathrm{KE}$ निर्धारित करें और दिखाएँ कि गैस को छोड़ने वाली उपकरण इस समय अवधि में कार्य करता है $=(1 / 2) \Delta m u^{2}$ (गुरुत्वाकर्षण को ध्यान में न लें)।

6.47 दो एक समान इस्पात क्यूब (द्रव्यमान $50 \mathrm{~g}$, पक्ष $1 \mathrm{~cm}$) आपस में मुख-मुख मिलते हैं और प्रति सेकंड $10 \mathrm{~cm} / \mathrm{s}$ की गति से टकराते हैं। प्रति क्यूब की अधिकतम संकुचन ढलान पता करें। इस्पात के लिए यंग का नियम $=Y=2 \times 10^{11} \mathrm{~N} / \mathrm{m}^{2}$।

6.48 वायु से भरे हुए गुब्बारे जब उठते हैं, तो उनकी संभावित ऊर्जा में वृद्धि होती है। गुब्बारे की गति भी बढ़ती है जब वह ऊपर उठता है। इसे यहां मैकेनिकी ऊर्जा के संरक्षण के साथ मेल कैसे करेंगे? आप वायु के घोर ऊर्ध्वाधर स्वरूप को ध्यान में नहीं रख सकते हैं और मान सकते हैं कि वायु का घनत्व स्थिर है।

समाधान 6

6.1 (ब)

6.2 (सी)

6.3 (ड)

6.4 (सी)

6.5 $\quad(सी)$

6.6 (सी)

6.7 (सी)

6.8 (ब)

6.9 (ब)

6.10 (ब)

6.11 (ब) जैसा कि विस्थापन $\alpha t^{3 / 2}$ होता है

6.12 (ड)

6.13 (ड)

6.14 (अ)

6.15 (ब)

6.16 (ड)

6.17 (ब)

6.18 (सी)

6.19 (ब), (ड)

6.20 (ब), (ड), (फ)

6.21 (सी)

6.22 हाँ, नहीं।

6.23 एलिवेटर को निकटतम के तहत गिरने से रोकने के लिए।

6.24 (अ) सकारात्मक, (ब) ऋणात्मक

6.25 सुचारू तथा समतल सड़क में अलग-अलग स्थानों पर लिए जाने वाला गुरुत्वाकर्षण शान्ति बुनियादी रूप से आधारभूत होता है।

6.26 नहीं, क्योंकि वायु की प्रतिरोधी बल भी शरीर पर कार्य करता है जो एक गैर-संरक्षकीय बल है। इसलिए, $\mathrm{KE}$ में बढ़ोतरी $\mathrm{PE}$ में हुई हानि से छोटी होगी।

6.27 नहीं, हर बंद मार्ग पर कार्य किया जाने वाला कार्यक्षमता केवल तभी शून्य होगी जब प्रणाली पर कार्य करने वाली सभी बलें संरक्षकीय हों।

6.28 (ब) कुल रैखिक प्राणि।

गेंदों के संपर्क में, उनमें विकृति हो सकती है जो किनेटिक ऊर्जा के हिस्से की तरह है। प्राणि हमेशा संरक्षित होती है।

6.29 शक्ति $=\frac{m g h}{T}=\frac{100 \times 9.8 \times 10}{20} \mathrm{~W}=490 \mathrm{~W}$

6.30 $P=\frac{\Delta E}{\Delta t}=\frac{0.5 \times 72}{60}=0.6$ वॉट्स

6.31 एक आपसी मात्रीकीय माघ्नेटिक क्षेत्र में चलता हुआ आपतित धारी।

6.32 कियोस्क द्वारा किया गया कार्य $=$ किनेटिक ऊर्जा का परिवर्तन

दोनों शरीरों की समान किनेटिक ऊर्जा होती है और इसलिए करने के लिए समान काम किया जाना चाहिए। क्योंकि लगाया गया बल समान है, इन्हें एक ही दूरी में आराम से रोक दिया जाएगा।

6.33 (अ) सीधी रेखा: ऊर्ध्वगामी, नीचे की ओर

(ब) परावृत्त रेखा जिसका मुद्रित रेखांश में शिरष है।

(सी) शिरष से ऊपर की ओर रखा परावृत्त रेखांश।

6.34

6.35 (अ) मुखों के बीच हेड-ऑन कोलिशन के लिए:

संरक्षण के अनुसार गतिशीलता $\Rightarrow 2 m v_{0}=m v_{1}+m v_{2}$

या $2 v_{0}=v_{1}+v_{2}$

और $e=\frac{v_{2}-v_{1}}{2 v_{0}} \Rightarrow v_{2}=v_{1}+2 v_{0} e$

$\therefore 2 v_{1}=2 v_{0}-2 e v_{0}$

$\therefore \quad v_{1}=v_{0}(1-e)$

चूंकि $e<1 \Rightarrow v_{1}$ की दिशा $v_{0}$ की तरह है, इसलिए गेंद संघर्ष के बाद आगे चलती है।

(b) गतिशीलता के अनुसार $\Rightarrow \mathbf{p}=\mathbf{p_1}+\mathbf{p_2}$

लेकिन $\mathrm{KE}$ खो जाती है $\Rightarrow \frac{p^{2}}{2 m}>\frac{p_{2}{ }^{2}}{2 m}+\frac{p_{2}{ }^{2}}{2 m}$

$\therefore p^{2}>p_{1}{ }^{2}+p_{2}^{2}$

इस प्रकार $\mathbf{p}, \mathbf{p_1}$ और $\mathbf{p_2}$ चित्र में दिखाए गए हैं।

$\theta$ अधिकृत है (यदि $\left.\theta=90^{\circ}\right)$ होता तो $\left(p^{2}=p_{1}{ }^{2}+p_{2}{ }^{2}\right.$ होता)।

6.36 क्षेत्र A : नहीं, क्योंकि $\mathrm{KE}$ नकारात्मक हो जाएगी।

क्षेत्र B : हाँ, क्योंकि कुल ऊर्जा शून्य गुणक योग्यता के बराबर हो सकती है।

क्षेत्र C: हाँ, यदि उसकी शाक्तिशाली ऊर्जा नकारात्मक हो।

क्षेत्र D : हाँ, क्योंकि शक्तिशाली ऊर्जा शून्य गुणक से बड़ी हो सकती है।

6.37 (a) गेंद A अपनी संपूर्ण गतिशीलता गेंद पर संकुचित करती है और कोई भी चढ़ाई नहीं करती है।

(b) $v=\sqrt{2 g h}=4.42 \mathrm{~m} / \mathrm{s}$

6.38 (a) प्रतिरोधकता का नुकसान $=m g h=1 \times 10^{-3} \times 10 \times 10^{-3}=10 \mathrm{~J}$

(b) $\mathrm{KE}=\frac{1}{2} m v^{2}=\frac{1}{2} \times 10^{-3} \times 2500=1.25 \mathrm{~J}$

(c) नहीं, क्योंकि कुछ हिस्सा $\mathrm{PE}$ हवा के छावनी द्वारा कार्य करने में उपयोग हो जाता है।

6.39 (b)

6.40 $m=3.0 \times 10^{-5} \mathrm{~kg} \quad \rho=10^{-3} \mathrm{~kg} / \mathrm{m}^{2} \quad v=9 \mathrm{~m} / \mathrm{s}$

$A=1 \mathrm{~m}^{2} \quad \mathrm{~h}=100 \mathrm{~cm} \Rightarrow n=1 \mathrm{~m}^{3}$

$M=\rho v=10^{-3} \mathrm{~kg}, E=\frac{1}{2} M v^{2}=\frac{1}{2} \times 10^{3} \times(9)^{2}=4.05 \times 10^{4} \mathrm{~J}$.

6.41 $\mathrm{KE}=\frac{1}{2} m v^{2} \cong \frac{1}{2} \times 5 \times 10^{4} \times 10^{2}$

$$ =2.5 \times 10^{5} \mathrm{~J} \text {. } $$

इसका 10% स्प्रिंग में संग्रहित होता है।

$$ \begin{array}{r} \frac{1}{2} k x^{2}=2.5 \times 10^{4} \ x=1 \mathrm{~m} \end{array} $$

$k=5 \times 10^{4} \mathrm{~N} / \mathrm{m}$.

6.42 6 $\mathrm{km}$ में 6000 सीढ़ियां होती हैं।

$\therefore E=6000(\mathrm{mg}) \mathrm{h}$

$$ =6000 \times 600 \times 0.25 $$

$$ =9 \times 10^{5} \mathrm{~J} \text {. } $$

यह प्राप्ति का 10% है।

$\therefore \quad$ प्राप्ति की ऊर्जा $=10 \mathrm{E}=9 \times 10^{6} \mathrm{~J}$.

6.43 $0.5$ कार्यक्षमता के साथ, 1 लीटर $1.5 \times 10^{7} \mathrm{~J}$ उत्पन्न करती है, जो 15 $\mathrm{km}$ यात्रा के लिए उपयोग होती है।

$\therefore F d=1.5 \times 10^{7} \mathrm{~J}$. यहां $d=15000 \mathrm{~m}$

$\therefore F=1000 \mathrm{~N}$ : घर्षण की शक्ति।

विषय: 6.44 (क) $W_{\mathrm{g}}=m g \sin \theta d=1 \times 10 \times 0.5 \times 10=50 \mathrm{~J}$।

(ख) $W_{\mathrm{f}}=\mu m g \cos \theta \quad d=0.1 \times 10 \times 0.866 \times 10=8.66 \mathrm{~J}$।

(ग) $\Delta \mathrm{U}=m g h=1 \times 10 \times 5=50 \mathrm{~J}$।

(घ) $a={F-(m g \sin \theta+\mu m g \cos \theta)}=[10-5.87]$

$$ =4.13 \mathrm{~m} / \mathrm{s}^{2} $$

$$ \begin{aligned} & v=u+a t \text { या } v^{2}=u^{2}+2 a d \ & \Delta K=\frac{1}{2} m v^{2}-\frac{1}{2} m u^{2}=\operatorname{mad}=41.3 \mathrm{~J} \end{aligned} $$

(च) $W=F d=100 \mathrm{~J}$।

6.45 (क) गोलों के लिए ऊर्जा संरक्षित होती है।

(ख) गोल नंबर 1 को घुमावणीय ऊर्जा प्राप्त होती है, जबकि गोल नंबर 2 घर्षण द्वारा ऊर्जा हार देता है।

वे निकटता कर सकते हैं सी पर पार नहीं कर सकते हैं। गोल नंबर 3 पार कर सकता है।

(ग) गोल नंबर 1, 2 सी पर पहुंचने से पहले मुड़ जाते हैं। ऊर्जा के नुकसान के कारण, गोल नंबर 2 ए तक वापस नहीं पहुंच सकता। गोल नंबर 1 जब यह ब तक पहुंचता है, तो वह एक घुमावणीय गति में होता है। यह ए के पास वापस झूल नहीं सकता है, क्योंकि यह गतिज घर्षण की वजह से लौट नहीं सकता।

6.46 $(K E)_{t+\Delta t}=\frac{1}{2}(M-\Delta m)(v+\Delta v)^{2}+\frac{1}{2} \Delta m(v-u)^{2}$

रॉकेट गैस

$(K E)_{t}=\frac{1}{2} M v^{2}$

$=\frac{1}{2} M v^{2}+M v \Delta v-\Delta m v u+\frac{1}{2} \Delta m u^{2} = W$

$KE_{t+\Delta t}-(KE)_{t}=(M \Delta v-\Delta mu) v\frac{1}{2} \Delta mu^2=\frac{1}{2} \Delta mu^2=W$

(कार्य-ऊर्जा के अनुसार)

क्योंकि $\left(\frac{Mdv}{dt}=\left(\frac{dm}{dt}\right)(|u|)\right) \Rightarrow(M \Delta v-\Delta mu)=0$

6.47 हुक का नियम: $\frac{F}{A}=\mathrm{Y} \frac{\Delta L}{L}$

यहां $\mathrm{A}$ सतह का क्षेत्रफल है और $L$ क्यूब के पक्ष की लंबाई है। यदि $k$ स्प्रिंग या संपीड़न स्थिर होता है, तो $F=k \Delta L$

इसलिए $\therefore k=Y \frac{A}{L}=Y L$

प्रारंभिक $कि=2 \times \frac{1}{2} m v^{2}=5 \times 10^{-4} \mathrm{~J}$

अंतिम $\mathrm{PE}=2 \times \frac{1}{2} k(\Delta L)^{2}$

$\therefore \Delta L=\sqrt{\frac{K E}{k}}=\sqrt{\frac{K E}{\mathrm{Y} L}}=\sqrt{\frac{5 \times 10^{-4}}{2 \times 10^{11} \times 0.1}}=1.58 \times 10^{-7} \mathrm{~m}$

6.48 आपातकालीन $m, V, \rho_{H e}$ को हेलियम गुब्बारे का द्रव्यमान, आयतन और घनत्व के रूप में इस प्रकार से दर्शाने का प्रयास करें और $\rho_{\text {air }}$ को हवा का घनत्व लें

गुब्बारे का आयतन V हवा का आयतन V को छीनता है

$$ \begin{equation*} यहां, तो \mathrm{V}\left(\rho_{\text {air }}-\rho_{H e}\right) g=m a \end{equation*} $$

तच्चन के साथ योग करने से,

$$ \begin{align*} & V\left(\rho_{\text {air }}-\rho_{H e}\right) g टी=m v \ & \Rightarrow \frac{1}{2} m v^{2}=\frac{1}{2} m \frac{V^{2}}{m^{2}}\left(\rho_{\text {air }}-\rho_{H e}\right)^{2} g^{2} t^{2}=\frac{1}{2 m} V^{2}\left(\rho_{\text {air }}-\rho_{H e}\right)^{2} g^{2} t^{2}

विषमल मूल्यनुमानको अनुक्रम र एकाग्रताको समस्या,

ल लिख्न गर्नुहोस् \ frac {1} {2} मे वी ^ {2} = \ left [वी (\ रो_ {ए} - \ रो_ {He} \ right) ग \ right]} \ left [\ लेख {1} {2 मे } \ वी (\ \ रो_ {ए} - \ \ रो_ {He} \ right) \ ग \ \त {2} \ right] \ \ \ = \ वी (\ रो_ {ए} - \ रो_ {He} \ right) \ ग \ ह

वर्गीयवेक गर्ने अनुक्रममा,

कृपया केही समय रोक्नुहोस्।

$ \Rightarrow \ frac {1} {2} मे वी ^ {2} + वी \ रो_ {\ text {हे}} \ ग \ ह = वी \ रो_ {\ text {वातावरण}} \ ह \ ग $

के ई बालूनको $ के ई_ {\ text {बालून}} पे_ {\ text {बालून}} $ बदल / बदलमा $ पे_ {वाताव रण} $र $ पे_ {बालूनको} $को बदलमा ।

त्यसरी, जब बालून माथि जान्छ, एक समान वातावरणको आने छोड्दछ, बालूनको $ पे_{बालूनको} $ र $ के_ई $ वृद्धि $ पे_{बालूनको} $ हेरेको मूल्य $ पे_{वातावरणको} $ मूल्य लागि [जसले निम्नमा आउँदछ]।